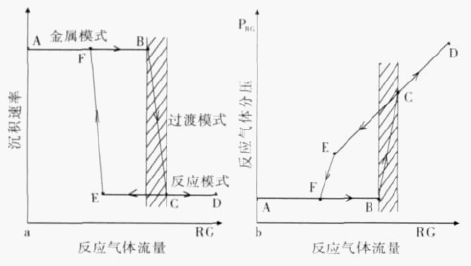
利用朗缪尔双探针诊断电弧离子镀等离子体参数
电弧离子镀于20世纪80年代兴起,是物理气相沉积( Physical Vapor Deposition,PVD) 技术的一个重要分支。基本原理是在真空条件下,靶源作为阴极、壳体作为阳极,利用阴极与阳极之间的弧光放电蒸发并电离靶材,产生等离子体,对样品进行沉积镀膜。电弧离子镀具有沉积速度快、金属离化率高、膜的附着力强、可镀材料广泛等优点,在工具钢刀具上有广泛的应用。
在电弧离子镀技术中,影响膜层质量的参数很多,如温度、靶电流、基片偏压等。针对用电弧离子镀制备某种材料薄膜时,通常需要对这些参数采用不同的值进行大量实验,通过镀膜参数与膜层性能之间的关系对制备工艺进行优化。在这方面电弧离子镀与其他薄膜沉积技术的研究方法是相同的。然而另一方面,在电弧离子镀研究中获得的工艺参数与膜层性能之间的关系很少象其他薄膜沉积技术,如磁控溅射等那样,在机理上得到解释。这使得研究人员对电弧离子镀微观过程的理解往往停留在假想层面上,从而使工艺参数的优化具有一定程度的盲目性。
造成这种情况的一个主要原因是到目前为止缺乏诊断电弧离子镀等离子体的有效手段。诊断等离子体参数常用的朗缪尔单探针在应用于电弧离子镀等离子体参数诊断时,会由于电弧离子镀等离子体非常高的密度,而使探针在接近电子饱和区时收集到很大的电流,从而使探针红热甚至发射电子而不能正常工作。另一方面,由于电弧离子镀等离子体非常不稳定,使测得的I-V 特性曲线非常不光滑,难以直接被用来分析得出等离子体参数。针对这些题,我们采用双探针方法,结合大量采样平均和离散傅里叶变换平滑处理,对诊断电弧离子镀等离子体进行了尝试,成功获得了薄膜制备条件下的平均等离子体密度和电子温度,从而找到了一种实用有效的诊断电弧离子镀等离子体的方法。实验结果有助于研究电弧离子镀等离子体参数与对薄膜生长影响的规律。
1、等离子体诊断原理
1.1、朗缪尔双探针原理
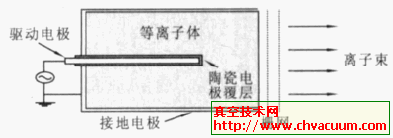
图1为双探针诊断等离子体的示意图。双探针由两个形状、尺寸、材料相同的金属电极组成, 探针电路与等离子体不共地。假设一个探针的电流为I1 ,另一个探针的电流为I2, I1 可以表示为:
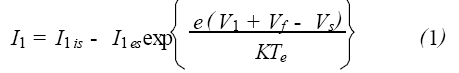
其中, I1is是探针1的饱和离子电流, I 1es是探针2 的饱和电子电流。V1是探针1 相对于悬浮电位Vf 的电位, Vs 是等离子体空间电位。由悬浮电位的定义式得
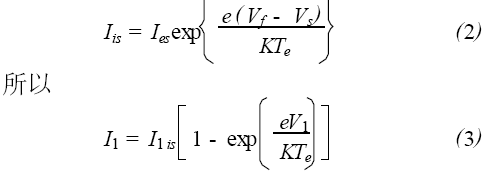
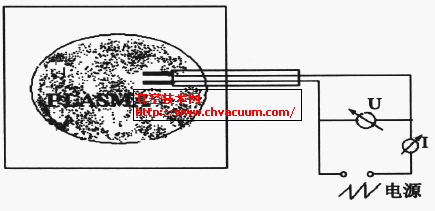
图1 双探针结构示意图
同理,可得探针2的电流表达式为
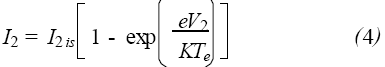
I2is是探针2的饱和离子电流, V2 是探针2 相对于Vf 的电位。由于双探针电路相对于等离子体处于“悬浮”状态,流入一个探针的电流与流出另一个探针的电流相等,所以I ≡I1 = - I2 。
当两探针完全相同时:
I 1is = I 2 is = Iis (5)
由式(3)~(5) 得:
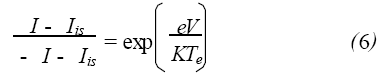
V = V1 - V2 是两探针间的电压。解等式(6) 得:
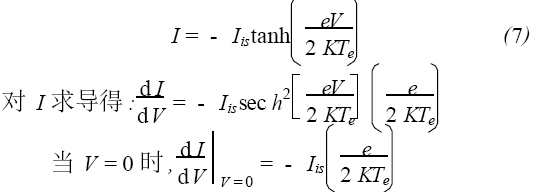
由上式可以看出:电子温度Te可以用V=0时双探针特征曲线的斜率求出。
由饱和离子电流的定义式得:
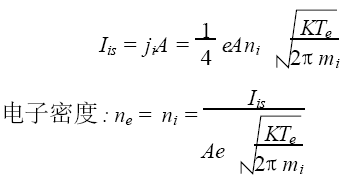
其中A 是探针面积, mi 是离子质量。
由公式(7)可以看出,双探针电流永远小于离子饱和电流,因此可以避免单探针诊断中出现的由于收集电流过大使探针红热甚至发射电子而不能正常工作的问题。
1.2、离散傅里叶变换平滑方法
如果用函数f(x) 表示测量数据f(0),f(1), ⋯,f 2N-1)的变化规律,f(x)可以展开成傅里叶级数形式
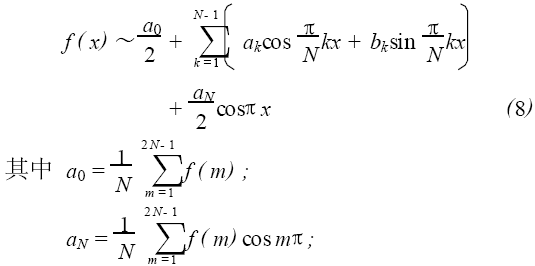
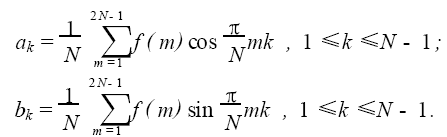
把函数f(x)可以写成如下形式
f(x)= f0(x)+N(x) (1)
其中, f0(x)表示测量数据内在的物理规律, N(x)表示噪音成分。可以证明函数越光滑或周期变化的规律性越好,其相应的傅里叶级数收敛越快。由于f0(x)通常是光滑连续的,而噪音N(x)本质上是无规则和不连续的,它们傅里叶展开的收敛性质不同:前者是收敛的,而后者不收敛。基于这种差别,如果在适当的位置( f0(x)已很好地收敛) 把f(x)的傅里叶级数截断并舍弃高频项,就可以大幅滤除噪音成分,从而使曲线变得光滑。