对普通矩形平面靶的磁场分布、电子运动轨迹和电子分布进行了理论计算。通过磁场的解析表达式，解出电子在磁场中的运动方程，求得并从理论上解释了电子的运动轨迹。由电子的运动轨迹，并运用Monte Carlo 方法，求得电子在磁场中的分布，得到电子分布的均值和标准差。本文通过在基片和靶材间加正向电场，改变了电子的运动轨迹和空间分布，优化了矩形平面靶的刻蚀形貌，提高了靶材利用率。

　　薄膜技术可有效而经济地改变零件表面功能，防止因磨损、腐蚀或氧化引起的失效，延长其使用寿命。而磁控溅射技术具有薄膜沉积速率高、膜层结合力好、基片温度低、靶材种类多等优点，可以制备工业上所需的超硬薄膜、耐腐蚀、耐磨擦薄膜、超导薄膜、光学薄膜以及各种具有特殊性能的膜，被广泛的应用在镀膜领域中。但是磁控溅射也存在一些显著的缺点，如靶材表面的不均匀刻蚀使靶材的利用率低。矩形平面磁控溅射靶是实际应用中一种比较常见的靶，所以本文对矩形平面磁控溅射靶面空间的电子分布进行了理论计算，并通过加正向电场的方法，改变了电子的运动轨迹和电子的空间分布，提高了靶材利用率。

1、矩形平面靶磁场的理论计算

　　1.1、矩形永磁体的磁场计算

　　在永磁体空间磁场的计算中，对于复杂的形体需要通过数值计算的方法得到其数值解，但对于简单的形体，如立方体，可通过等效电荷法或等效电流法求得其解析表达式。苟晓凡博士推导出的矩形永磁体外部磁场的解析表达式，可以比较简单地表达永磁体的外磁场，所以本文运用此方法对磁控溅射矩形平面靶磁场进行了数值计算。

　　如图1 所示的矩形永磁体，其外部空间磁场分布的解析表达式为

图1 矩形永磁体

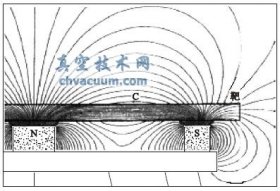
图2 磁控溅射示意图

5、结论

　　(1) 本文通过矩形永磁铁的解析表达式，提出球面寻优法计算得到了矩形磁控溅射靶5 块永磁体形成的磁场分布。

　　(2) 运用Matlab 中的变步长龙格库塔算法，求解了电子在电磁场中的运动方程，并得到电子的运动轨迹。

　　(3) 运用Monte Carlo 方法对电子的散点图进行整理，得到电子分布直方图。

　　(4) 由于电子碰撞的数学模型现在还不是很清晰，所以本文没有考虑电子间的碰撞。

　　(5) 通过理论分析得到，在靶材刻蚀最深处加正向电压，可有效优化电子运动轨迹及其分布。

　　(6) 本文所加的正向电场大小和位置没有经过理论计算，仅通过模拟得到。