使用氦质谱吸枪检漏法检测航天器管路双密封结构螺接头漏率时，常会发生漏率随时间变化的情况。为了从理论上分析该问题的实质，本文建立了两种双密封结构泄漏过程的数学模型，分别考虑了分子流和粘滞流两种状态，并求解了数学模型的方程解析解，编制程序进行数值模拟仿真，形象地显示了双密封结构系统正压泄漏情况下，漏率、压力与泄漏时间关系的规律，及其影响泄漏时间长短的因素。并计算了不同初始条件下，双密封结构的漏率稳定时间。这些研究结果可直接应用于航天器管路双密封结构螺接头漏率测试候检时间评估计算，并对双密封结构系统的设计和泄漏安全评估，从理论上提供指导意义。

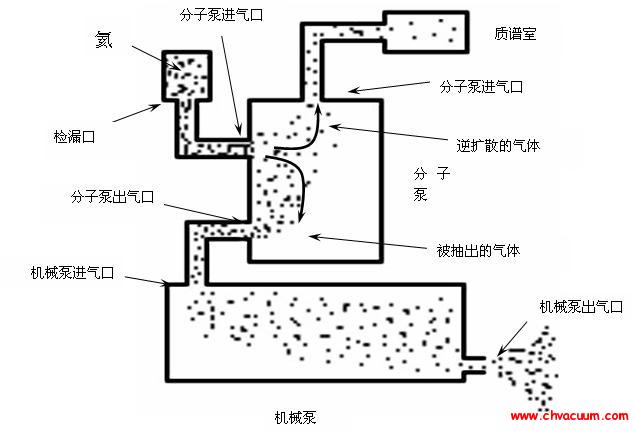
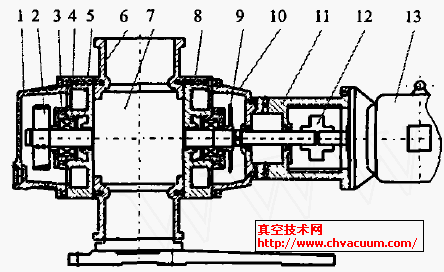
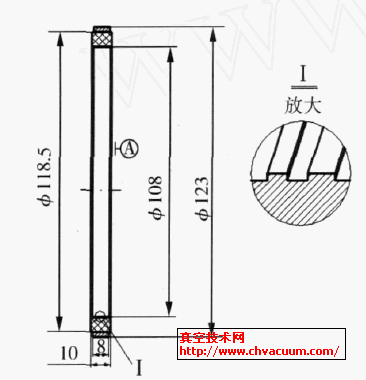
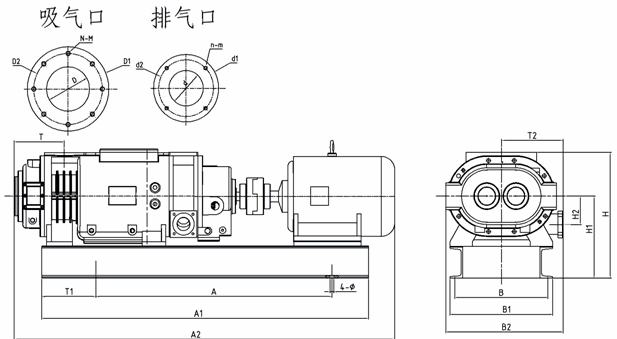
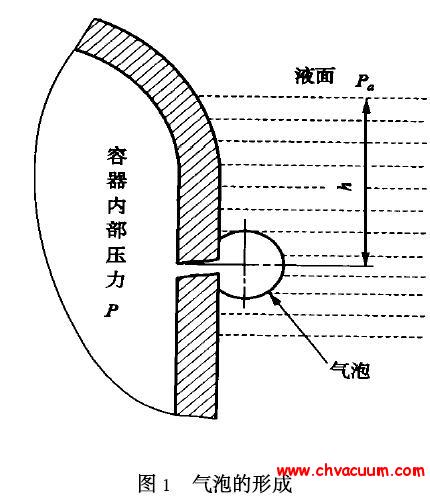
　　航天产品管路系统的连接方式常用柱塞式密封接头形式(如图1 所示)，该密封方式由两道密封环节组成，属于典型的双密封结构。在使用氦质谱检漏仪对密封接头进行吸枪单点检漏或者真空法检漏时，都会出现测试漏率缓慢升高的现象，并且缓升的时间长，难以确定具体读数时间。这是由双密封结构的泄漏特点决定的，泄漏介质首先经过第一道密封环节进入双道密封之间的空间，然后再经过第二道密封环节进入外界环境，被检漏仪检测。泄漏过程与双道密封之间空间的体积、密封环节漏率、介质压力等等有关系，因此真空技术网(http://www.jnannai.com/)认为有必要从理论和数值模拟仿真分析该泄漏过程，为合理的读取数据，确定产品漏率提供依据。

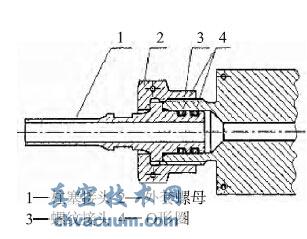
图1 密封方式原理图

　　1、数学模型建立

　　1.1、数学模型参量定义

　　根据双密封结构的泄漏特点，假定从纯氦端流入容积V 的氦气会迅速扩散，不计算扩散时间(因扩散时间远小于观察时间)。理论设定的模型示意图如图2，参数参量与解释见表1。考虑泄漏过程的不同流态，可以分为分子流和粘滞流两种流态下进行数学模型建立。

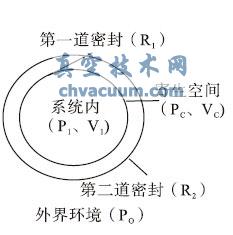
图2 双密封结构示意图

　　1.2、分子流流态下数学模型

　　当考虑漏孔泄漏过程为分子流流态时，漏孔的漏率与漏孔两端压力差成正比，因此可有如下分析：

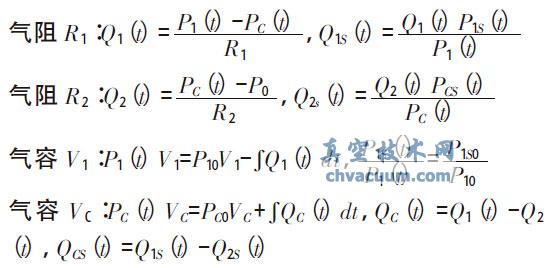
2、结语

　　目前对于双密封结构漏率检测的候检时间确定，稳定漏率的判断存在较大的困难。本文主要通过对典型双密封结构进行简单的模型建立、理论分析和数值仿真，揭示了双密封结构中各个因素对漏率稳定时间影响的规律。实际应用中可首先初步判断双道密封环节的初始漏率，再利用数值仿真程序对漏率检测候检时间进行初步计算和判断，以此来指导时间的检漏过程，提高检漏数据的准确度，并在指导双密封结构系统的设计和泄漏安全评估方面具有重要意义。