针对现有某离心泵效率低和扬程曲线存有驼峰的现象，利用遗传算法优化相关结构参数，得到满足要求的叶片数、出口宽度、出口安放角及叶轮外径。通过对比分析定常多相位法和非定常法结果与试验值的误差，发现定常多相位法的精度更高。在此基础上运用定常多相位法验证了遗传算法优化模型能有效提高效率，且H-Q曲线无驼峰。

一、前言

　　离心泵作为一种应用广泛的通用机械，在工业及城市供水、排水和农业灌溉等方面发挥着重要的作用。传统的设计方法难以快捷、准确地达到目标，为满足不同的需求，合理地设计和改型至关重要。遗传算法作为智能优化的一种，因其思想简单，易于实现而被应用于各类结构的设计和优化中。但在离心泵的设计和优化上，遗传算法的应用尚且不多。W.A.Wahba等人第一次将遗传算法引入到离心泵叶片优化设计中，并取得了较为理想的结果;闫永强等人对遗传算法在流体机械优化设计中的应用现状做了总结，并分析了其在离心泵优化问题中应用的可行性;何希杰等人评价了遗传算法和传统设计方法在离心泵设计上的优势，认为其易于实现，且效果显著。

　　同时，由于试验往往消耗大量的人力、物力，各种研究成果的可行性难以被证实。而CFD数值模拟方法因其高适应性和准确性受到广大学者认可。因此，本文将遗传算法与CFD数值模拟相结合，以某型清水离心泵为研究对象，建立数学模型，利用遗传算法得到满足要求的叶片数、出口安放角、出口宽度和叶轮外径。通过比较两种数值模拟方法与试验值的误差，验证了多相位定常法可以预测离心泵的性能，在此基础上考察了离心泵优化前后的性能。

二、遗传算法优化设计

　　遗传算法是一种模拟生命进化机制的一种搜索与寻优方法，它借鉴达尔文的物竞天择、适者生存的自然选择和自然遗传机理，形成了一种求解问题的高度并行全局搜索方法，真空技术网(http://www.jnannai.com/)认为与传统方法相比，具有更强的全局寻优能力。

　　作为智能算法的一种，遗传算法的运算是基于由一系列数列组成的染色体，并根据适者生存的原理，采用选择、杂交和变异对染色体中的数值进行更新。

　　1. 优化设计的数学模型

　　现有离心泵的主要参数见表1。

表1 现有离心泵的主要参数

　　离心泵的实际扬程为理论扬程与水力效率的乘积。理论扬程Ht的计算 ：

　　式中 μ ——出口的滑移系数，μ =1-πsinβ 2/Z;Z——叶片数;β2——出口安放角;Ψ 2——叶片出口排挤系数;b2——出口宽度。

　　离心泵的水力效率η h，容积效率η v，机械效率η m计算如下：

　　本文以叶片数Z，出口宽度b2，叶片出口安放角β2，叶轮直径D2作为设计变量，离心泵的效率作为第一分目标函数：

　　由于较小值的Z、β2、b2和较大值的D2可以有效避免H—Q曲线的驼峰现象，因此，在目标函数中加入第二分目标函数，以提高具有这些基因的个体的适应度。

　　同时定义叶片数与叶片出口角的关系，设立式(8)为约束条件，对不满足式(8)的个体，定义其适应度为0，以降低可能造成驼峰现象的个体被选择的概率。利用线性加权和法建立如式(7)所示总的目标函数：

　　其中，ω 1、ω 2为加权系数，在式(7)中均定义为0.5。α 为调节因子，用以调节两个分目标函数的数量级，此处定义为10。

　　2. 个体编码

　　由于遗传算法不能直接处理十进制数，将各参数转换为二进制，且每5位二进制数表示一个参数。x (1)= Z，x (2) = b2，x (3) =β2，x (4) = D2。一组由20位二进制数组成的代码表示一个个体基因。选择300个个体作为该种群的初始种群数。选择概率、杂交概率和变异概率分别为0.2、0.9、0.05。在进化200代以后，从300个个体中筛选出具有最高适应度的个体，得到的结构参数见表2。图1为各代的最大适应度和平均适应度。

表2 设计参数对比

图1 各代平均与最佳适应度

　　从图1可以发现，随着进化过程，个体的最佳适应度不断上升，并在进化10代后保持稳定。而平均适应度在60代以前呈上升趋势，60代以后，在一定范围内波动。这是因为复制、变异的存在，新物种仍不断出现的缘故。图2为第1、25、100、200代个体的适应度分布，其中第一代种群中仍存在着大量的不适应环境的个体(不满足约束条件，适应度为0)，个体的适应度分布也相对分散。随着进化代数的增加，个体向最有利生存的基因发展，不适应环境的个体逐渐减小，个体的适应度往高处聚集。

图2 搜索过程中各代的适应度分布

三、数值模拟计算与分析

　　1. 原模型的数值模拟与可靠性评价

　　由于试验通常花费较大，本文采用CFD数值仿真，基于Fluent数值模拟考察遗传算法优化后离心泵的性能。采用多相位定常法和非定常法对优化前离心泵的扬程和效率值进行计算，通过与试验值的对比，对模拟方

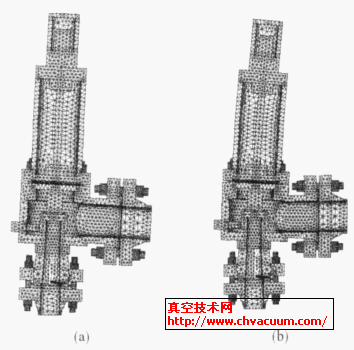
　　法的可靠性进行评价。首先，利用SolidWorks软件建立离心泵的三维模型，叶轮、蜗壳及其装配如图3所示，延长蜗壳出口以减少边界条件泵内流场的影响。

图3 离心泵三维造型

　　分别用定常多相位法和非定常法模拟计算离心泵内部流场，其中非定常法是基于动静域之间的滑移网格。定常多相位示意如图4所示。

图4 多相位定常法示意

　　由于叶轮旋转时，叶轮和蜗壳相对位置呈周期性不断变化，扬程和效率值也受到了影响。为了准确获得这种瞬态现象，模拟计算不同相对位置下的流场。每个相对位置是一个相位。由于优化前的离心泵有6个叶片，叶轮旋转一周即为6个周期，定义每10°为一个相位，一个周期即为6个相位。考虑到离心泵结构的复杂性，采用ICEM CFD软件划分非结构体网格如图5所示，网格质量满足Fluent计算要求。叶轮和蜗壳的网格数分别为700 661和212 766。定义进口为速度进口，速度方向为轴向，并根据流量计算速度值。定义出口边界为自由出流。采用标准k—ε 湍流模型，压力和速度耦合采用SIMPLEC算法，动量方程、湍动能和耗散率输运方程的离散采用二阶迎风格式。

图5 网格划分

　　针对6个工况下扬程和效率，试验数据与模拟数据的比较如图6所示。非定常法在小流量和大流量的扬程均低于试验值，而在设计工况附近，均高于试验值。定常多相位法在大流量下，扬程低于试验值，在小流量和设计工况附近均较高。对于效率，三类数据呈相同的变化趋势，其中模拟值在大流量下低于试验值，在小流量和设计工况附近均高于试验值。两种模拟方法与试验值的误差见表3。

图6 离心泵性能对比

表3 误差对比(单位：%)

　　根据图6和表3可发现，定常多相位法获得的模拟值与试验值具有较好的吻合度。

　　2. 优化模型的性能计算

　　建立优化后的离心泵模型，利用定常多相位法模拟计算其性能，如图7所示。在设计工况下，效率值为56.7%，较优化前的效率52.9%有所上升，且完全消除了H—Q曲线的驼峰现象。

图7 优化后离心泵的性能曲线

四、结语

　　采用遗传算法对现有离心泵模型进行了结构优化，在分析比较数值模拟方法准确性的基础上，对优化后的离心泵性能进行了模拟，结果显示遗传算法得到的结构参数满足要求，并得到以下结论。

　　1)应用遗传算法优化离心泵的结构，通过建立数学模型，获得了优化的结构参数Z=4，b2=4，β 2=16，D2=0.198。其过程简易，整个计算过程依托于算法程序，相比于传统设计方法更为省时省力。

　　2)分析比较了定常多相位法和非定常法对离心泵内部流场的适用性及Fluent模拟计算的准确性，通过与试验值的对比，发现定常多相位法计算得到的扬程和效率更为接近试验值。

　　3)利用定常多相位法考察优化后的离心泵模型性能，该模型的效率较优化前上升3.8%，且消除了H—Q曲线的驼峰现象。