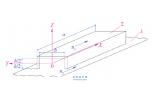
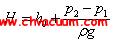双级滑阀泵运动系统的动力分析与动平衡
双级滑阀泵机构运动的力学模型
滑阀泵的运动核心部件是曲柄摇块机构, 工作时会引起惯性力, 包括偏心转子和滑阀环不平衡质量的回转离心惯性力以及滑阀杆的惯性力, 它们是滑阀泵振动的主要原因。为了减少滑阀不平衡惯性力引起的振动, 通常双级滑阀泵的动平衡结构有两种: 两缸和三缸。国外以美国KINNY 公司为代表,以三缸结构为主体发展单级和双级滑阀真空泵, 依靠长缸和两个短缸相互之间消除不平衡惯性力和惯性力矩, 这一结构具有较好的动平衡效果, 不需要在皮带轮上加配重, 不需要加平衡轮, 但三缸泵滑阀转子结构固定, 所以剩余惯性力是固定不变的, 很难再进行优化降低。而双缸泵通过平衡轮可优化配重,平衡效果优于三缸泵, 本文对两缸结构进行动平衡分析, 对两级滑阀泵体产生的不平衡惯性力加平衡配重, 以达到减小不平衡惯性力、降低振动的目的。

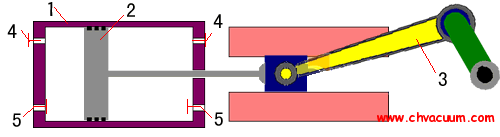
图1 双缸滑阀泵平衡结构图
两缸结构中, 长短缸相位相差180设置, 两者长度比一般为2: 1, 再在驱动轮上加上平衡配重, 如图1 所示。两缸结构的难点在于必须通过较复杂的平衡计算, 长缸存在滑阀、偏心轮产生的离心惯性力,短缸也存在偏心轮和滑阀产生的离心惯性力, 同时长缸、短缸的滑阀杆也存在离心惯性力, 再加上平衡配重的离心惯性力, 则组成相当复杂的空间力系。图2 给出了两缸结构的平衡空间力系图, B1、B11、B111为泵轴中心, A1、A11 分别为长短偏心轮中心, A1O1、A11O11 分别为长短滑阀, W为泵轴转速; F0 为长偏心轮离心惯性力, F01 为短偏心轮离心惯性力, Fx 、Fy分别为长滑阀不平衡惯性力X 、Y 轴向分力, Fx1、Fy1分别为短滑阀不平衡惯性力X 、Y 轴向分力, Fx11、Fy11分别为平衡轮离心惯性力X 、Y 轴向分力。

图2 双缸泵空间力系图
从图2 可以得出, 整体双缸结构的双级滑阀泵的不平衡惯性力的计算公式为

惯性力幅值的最小二乘拟合
由方程(1) 可知, 只要计算平衡配重与泵两缸产生的不平衡惯性力在所有位置上的合力, 即![]() 就可以使作用于整个双级泵的振动减至最小。所以,对于平衡配重所产生的惯性力是整个振动平衡计算的关键, 为了寻求最佳的平衡效果, 提出多级平衡的新概念。配重所产生的惯性力是按照一阶简谐运动变化, 而长短缸在运动中所产生惯性力的大小和方向随时都改变着, 需要在不同方向配置相应的平衡配重, 即采用多级平衡配重,使泵的剩余惯性力渐次逼近最小值以获得最优的平衡效果。因此计算双缸结构的双级泵的动平衡, 最主要的就是各级配重质量、重心及其分布的确定。这里引入了最小二乘法, 将各级配重的惯性力的简谐运动变化的目标曲线来拟合所计算出的长短缸的惯性力曲线, 使作用于泵体上的不平衡惯性力趋于最小, 从而计算出各级配重最优的质量和质心。
就可以使作用于整个双级泵的振动减至最小。所以,对于平衡配重所产生的惯性力是整个振动平衡计算的关键, 为了寻求最佳的平衡效果, 提出多级平衡的新概念。配重所产生的惯性力是按照一阶简谐运动变化, 而长短缸在运动中所产生惯性力的大小和方向随时都改变着, 需要在不同方向配置相应的平衡配重, 即采用多级平衡配重,使泵的剩余惯性力渐次逼近最小值以获得最优的平衡效果。因此计算双缸结构的双级泵的动平衡, 最主要的就是各级配重质量、重心及其分布的确定。这里引入了最小二乘法, 将各级配重的惯性力的简谐运动变化的目标曲线来拟合所计算出的长短缸的惯性力曲线, 使作用于泵体上的不平衡惯性力趋于最小, 从而计算出各级配重最优的质量和质心。
设i 时泵轴转角为ai (0℃到360℃依次取值) , 长短缸的不平衡惯性力为F 1(i) , 滑阀泵X 、Y 方向的剩余惯性力Fx (i) 和Fy (i) 分别为

式中, m 为总的配重级数, W 为泵轴转动角速度(r/s) ; M(k) 为第k 级平衡配重的质量(kg) ; E(k) 为第k 级平衡配重的质心值(mm) (平衡配重的质心到旋转轴中心的径向值) ; F 1x (i) 为a i 转角时X 方向的长短缸不平衡惯性力差值(N) ; F1y (i) 为a i 转角时Y 方向的长短缸不平衡惯性力差值(N) 。
这是非线性函数的曲线拟合问题, 采用高斯-牛顿法进行曲线拟合。针对双级滑阀泵剩余不平衡惯性力在X 、Y 方向建立的非线性最小二乘拟合的目标方程(2)、(3), 参数初值的选取是通过求解m个矛盾方程组, 得到k 级配重M(k) 和E (k) 的样本估计值, 作为参数的初值。最后令![]() 求出各级配重M(k) 和E (k) 值。
求出各级配重M(k) 和E (k) 值。