动叶轮作为分子泵的关键部件，与芯轴过盈装配，要求在高速状态下仍保持一定的过盈量。本文计算了动叶轮在高速转动时的径向变形、过盈装配时的初始应力状态和转动时应力状态，根据径向变形量的差异和应力优化了装配过盈量，既保证了动叶轮转子强度又使过盈联接可靠。

　　分子泵作为获得洁净真空环境的重要设备在现代工业中得到了越来越广泛的应用，高速、小型化是其发展方向之一，最高转速达到90000 rpm^[1]。分子泵的动叶轮通常与芯轴过盈联接，并要求在任何状态下保持一定的过盈量。如果初始过盈量太小，在高速转动时，动叶轮内圈的径向变形量大于转子的径向变形量，当二者的差值大于初始过盈量时，两者会发生相对滑动而发生破坏。但如果过盈量太大，装配产生的预应力会造成动叶轮开裂。因此，真空技术网(http://www.jnannai.com/)认为设计合理的装配过盈量，对于保证结构的可靠运行具有十分重要的意义。

1、动叶轮和芯轴径向变形计算

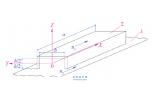
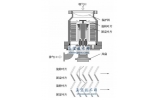
　　分子泵叶轮结构如图1 所示，叶轮共有六级，倾角分别为40°(1 片)、30°(2 片)、20°(3 片)，它们通过过盈装配的方式与芯轴联接。动叶轮材料为铝合金，弹性模量E=70 GPa，泊松比μ=0.33，密度ρ=2770 kg/m³。芯轴材料为不锈钢，弹性模量E=193 GPa，泊松比μ=0.31，密度ρ=7750kg/m³。

图1 分子泵叶轮结构示意图

　　计算单个零件在最大设计转速30000 r/min下的变形情况^[2]。20 度叶轮的径向变形如图2 所示，其内圈的径向伸长量约为8μm。30°叶轮和40°叶轮的径向伸长量分别为6μm和5μm。芯轴的径向变形如图3 所示，其与20°叶轮联接部分的径向伸长量约为0.6μm，与30°叶轮和40°叶轮联接部分的径向伸长量约为2.3μm。可见，20°、30°和40°动叶轮与芯轴的径向变形差分别为7.6μm、3.7μm、2.7μm。

图2 20°叶轮的径向变形　图3 芯轴的径向变形

2、动叶轮和芯轴的装配应力计算

　　根据上述计算结果，20°、30°、40°叶轮的单边过盈量分别取10μm、6μm、5μm。计算在该过盈量下叶轮转子结构的装配应力^[3]，结果如图4 所示。

图4 动叶轮的装配应力

　　20°叶轮的最大等效应力约为62.8 MPa;30°叶轮的最大等效应力约为33.6 MPa;40°叶轮的最大等效应力约为25.7 MPa;转子的最大等效应力约为23.6 MPa。最大应力均产生于动叶轮与芯轴的联接处，而叶片上应力很小。

3、离心力与装配应力合成效果分析

　　分子泵叶轮转动时离心力会使结构产生应力和变形。在最高转速下，装配预应力和离心力的共同作用使结构产生如图5 所示的等效应力状态。20°叶轮的最大等效应力约为61.8 MPa;30°叶轮的最大等效应力约为40.1 MPa;40°叶轮的最大等效应力约为31.1 MPa;转子与叶轮连接面上的最大等效应力约为37.7 MPa。

图5 装配应力和离心力共同作用的等效应力

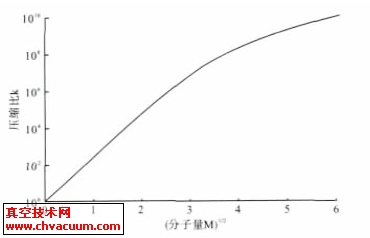
　　叶轮转动产生的离心力一方面会使结构产生应力，另一方面会使动叶轮产生大于芯轴的径向变形而减小接触应力，二者的综合作用使结构在最高设计转速内各部件的等效应力没有随着转速增加而显著增大。该结论可从图6 等效应力随着转速的变化关系中得到印证。设计的装配过盈量一方面保证了结构的可靠连接，另一方面没有使结构的等效应力显著增加，是较为合理的。

图6 等效应力随着转速的变化关系

4、结语

　　计算了分子泵动叶轮和芯轴转动时的径向变形，根据其径向变形量的差异设计了装配过盈量，并计算了在该过盈量下结构的初始应力状态和转动应力状态，保证了叶轮和芯轴强度足够并且连接可靠。

参考文献

　　[1] 巴德纯，王晓东，刘坤，等.现代涡轮分子泵的进展[J].真空，2010,47(4)：1- 6.

　　[2] 郁晋军，张君安，刘敏强，等.复合分子泵转子离心变形与热应变的有限元分析[J].真空，2011,48(1)：51- 53.

　　[3] 浦广益.ANSYS Workbench 12 基础教程与实例讲解[M].北京：中国水利水电出版社，2010：205- 209.